Geometria analítica Da superfície cónica de revolução às secções cónicas Parte 1 : A superfície cónica de revolução

Tal como prometi da última vez, vamos lá deduzir a equação de uma superfície cónica de revolução.
Para isso, consideremos um ponto V no semieixo positivo Oz, de coordenadas (0, 0,a), e uma circunferência de raio r centrada na origem e contida no plano xOy.
A superfície cónica (de revolução) é o conjunto de todos os pontos de todas as rectas que passam por V e por um ponto arbitrário de .
Vamos lá escrever isto com equações.

A forma geral de um ponto de pode ser (r cos θ,r sin θ, 0) onde θ [0, 2π[. Uma equação vectorial de uma recta que passa em V e por um ponto de é

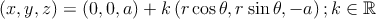
Logo, uma equação paramétrica desta superfície cónica é

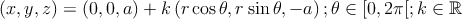
Vou tentar eliminar os parâmetros k e θ e obter uma equação em x,y,z,a e r. Esta equação paramétrica pode reescrever-se assim

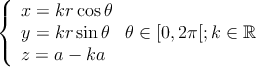
E isto implica que:

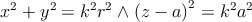
(Se elevarmos ao quadrado as duas primeiras equações "do sistema"e somarmos temos a primeira igualdade. Se na 3^a equação "do sistema"passarmos a para o primeiro membro, e depois elevarmos cada membro ao quadrado temos a 2^a equação) E daqui rapidamente se tira

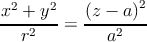
(deixo a justificação e algumas tecnicidades a cargo do leitor)

Fazendo uma translação de toda a superfície por forma a que V coincida com a origem do referencial, ficamos com a equação:

continua num próximo post

Algumas observações:
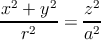
A técnica aqui usada pode ser aplicada para deduzir muitas outras equações de superfícies cónicas não necessariamente de revolução, e até de outras superfícies que nada têm a ver com cones. Como sai do âmbito do que tenciono fazer nesta exposição, por enquanto deixarei isto apenas como nota.
Tal como prometi, é um exercício "infantil" (não é?). O próximo post sobre este tema é também simples...
Quem tem conhecimentos suficientes de cálculo integral pode utilizar a equação da superfície cónica aqui deduzida para fugir um bocadinho ao assunto e deduzir a fórmula do volume do cone que todos conhecemos (ou devíamos conhecer) do ensino pré-universitário.
Ainda não sei quando postarei as próximas partes sobre este desenvolvimento relativamente a cónicas, mas tentarei fazê-lo brevemente.