Aviso: Nesta dedução, por comodidade, os pontos são confundidos com os
seus vectores posição.
O incentro I de um triângulo é o ponto de intercecção das três bissectrizes dos angulos internos.
Se as três encontram-se no mesmo ponto então, basta determinar a intersecção de duas destas três semi-rectas.

Sejam A;B e C os vértices de um triângulo. Como é normal fazer, denominemos por a o lado oposto a A,b o lado oposto a B e c o lado oposto a C.
Como mostrei há duas (quase três) semanas , a equação da bissectriz de ∠BAC é
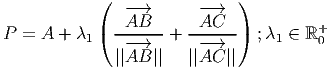
Ou, de forma equivalente
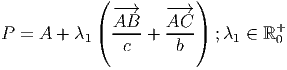
Uma equação vectorial da bissectriz de ∠ABC é
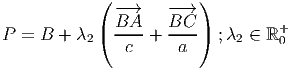
A intersecção é:
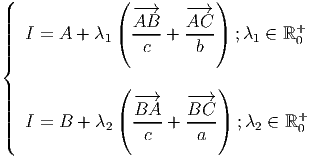
Logo
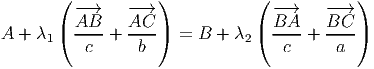
Ou, equivalentemente
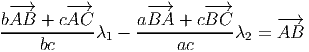
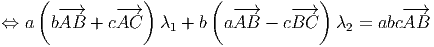
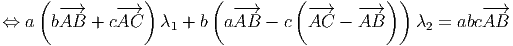
![-→ -→ -→
⇔ [abλ1 + (ab + bc)λ2]AB + (ac λ1 - bcλ2 )AC = abcAB](http://4.bp.blogspot.com/-gXpFT4qmuxc/UyW3usodF_I/AAAAAAAADDw/SLZ9Owi76zk/s1600/201403168x.png)
Sendo esta última igualdade verdadeira temos de ter
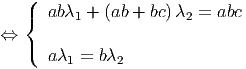
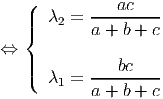
E portanto
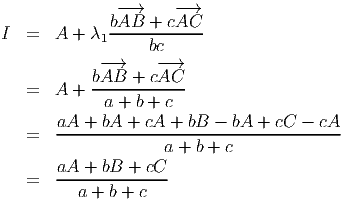
A duas dimensões, temos então
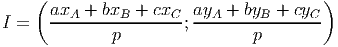
onde p é o perímetro do triângulo.
E a três dimensões temos
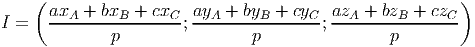
![CarlosPaulices no século XXI [até 2019]](https://2.bp.blogspot.com/-ZZaGUx4zRuY/VforUatAmuI/AAAAAAAAEEY/LcFBbgQUPXk/s1600-r/letras.png)

Sem comentários:
Enviar um comentário