
quarta-feira, 31 de dezembro de 2014
Feliz 2015 a todos

terça-feira, 23 de dezembro de 2014
O Caderno...
Num desses pdf (Casio1999.pdf) tenho vários programas para calculadoras, (por exemplo os jogos Batalha Naval e CPmissil).
No entanto, nesse pdf está apenas o código não comentado dos programas (pois, as calculadoras têm um limite de memória que na altura me fazia tentar escrever o mínimo possível).
Transportei ambos os jogos para calculadoras recentes, (Nomeadamente, máquinas Casio fx-9860 e casio-Fx-CG20) E preparo-me para escrever versões mais recentes de ambos os programas no sdk oficial da Casio para a FX9860-G.
Ainda não está nos meus planos uma versão nova para CG-20, embora se justificasse (Nesta calculadora os jogos conseguem ser mais lentos do que para as calculadoras em que foram programados originalmente)
Na altura, quando escrevi os programas, tinha um caderno onde tomava registo de todos os raciocínios e variáveis , pois, naquelas máquinas todas as variáveis são globais, e portanto esse tipo de cuidado era necessário... Se o caderno ainda existir, um dia, deixo uma nova versão, dedicada ao pessoal que quiser aprender a programar coisas simples ou com uma complexidade limitada, na calculadora.
[Nessa altura, posso ainda transportar alguns dos programas para TI-83/84plus..]
terça-feira, 9 de dezembro de 2014
Intersecção de Circunferências em coordenadas rectangulares
Parte 2: A circunferência e a recta (I)
Sejam C(x1,y1) e M(x2,y2). Pretendo determinar os pontos de intersecção das
circunferências de centro C e raio R1 e de centro M e raio R2, se
existirem.
Portanto, pretendo obter uma expressão para as soluções do sistema
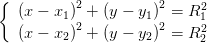
Desenvolvendo as equações temos:

E subtraindo a segunda equação da primeira temos:
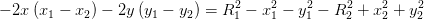

Esta última equação, é a equação de uma recta r que contem os pontos
da intersecção das circunferencias. A equação mostra-nos que a recta r é
perpendicular a CM, pois um vector ortogonal à recta é  Que
é vector director de CM! Seguindo o exemplo que dei na primeira parte, para
obter as coordenadas dos pontos de intersecção, se existirem, basta intersectar
esta recta com uma das circunferências.
Que
é vector director de CM! Seguindo o exemplo que dei na primeira parte, para
obter as coordenadas dos pontos de intersecção, se existirem, basta intersectar
esta recta com uma das circunferências.

Resolver um sistema deste tipo é algo que até se faz bem... com números! Vamos lá espreitar o caso geral da intersecção de uma circunferência com uma recta:



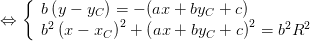


Não sei o leitor, mas a última equação já me dá alguma vontade de
recorrer a um programa de computação algébrica, embora não sejam
cálculos complicados.
No entanto como eu de vez em quando digo, quando se trata de implementação computacional,
"por mais monstruosa que seja a fórmula...será o computador a tratar dela."
Note-se que no problema original da intersecção de circunferências o nosso a²+b² é o quadrado da distância entre os centros das circunferências.
![CarlosPaulices no século XXI [até 2019]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgU5BEd9Lsy0qPx7MlTx5t-XAJeXYqWCwD-HemY9YHUezWhJqZUXnJGsyqAOK2ZsFkfr6mIyyUxhpsI_umhtq0TvNbxPvgGLXEJDrDh8bypa6gyv8YtdkiwDo92uRYGJreFcn7JhyphenhyphenUPYWk-/s1600-r/letras.png)
