Sejam C(x1,y1) e M(x2,y2). Pretendo determinar os pontos de intersecção das
circunferências de centro C e raio R1 e de centro M e raio R2, se
existirem.
Portanto, pretendo obter uma expressão para as soluções do sistema
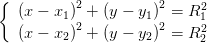
Desenvolvendo as equações temos:

E subtraindo a segunda equação da primeira temos:
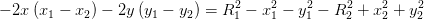

Esta última equação, é a equação de uma recta r que contem os pontos
da intersecção das circunferencias. A equação mostra-nos que a recta r é
perpendicular a CM, pois um vector ortogonal à recta é  Que
é vector director de CM! Seguindo o exemplo que dei na primeira parte, para
obter as coordenadas dos pontos de intersecção, se existirem, basta intersectar
esta recta com uma das circunferências.
Que
é vector director de CM! Seguindo o exemplo que dei na primeira parte, para
obter as coordenadas dos pontos de intersecção, se existirem, basta intersectar
esta recta com uma das circunferências.

Resolver um sistema deste tipo é algo que até se faz bem... com números! Vamos lá espreitar o caso geral da intersecção de uma circunferência com uma recta:



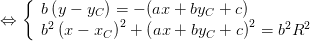


Não sei o leitor, mas a última equação já me dá alguma vontade de
recorrer a um programa de computação algébrica, embora não sejam
cálculos complicados.
No entanto como eu de vez em quando digo, quando se trata de implementação computacional,
"por mais monstruosa que seja a fórmula...será o computador a tratar dela."
Note-se que no problema original da intersecção de circunferências o nosso a²+b² é o quadrado da distância entre os centros das circunferências.
![CarlosPaulices no século XXI [até 2019]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgU5BEd9Lsy0qPx7MlTx5t-XAJeXYqWCwD-HemY9YHUezWhJqZUXnJGsyqAOK2ZsFkfr6mIyyUxhpsI_umhtq0TvNbxPvgGLXEJDrDh8bypa6gyv8YtdkiwDo92uRYGJreFcn7JhyphenhyphenUPYWk-/s1600-r/letras.png)

2 comentários:
Jorge Lourenço:
Sugiro aplicar uma tranlação seguida de uma rotação que coloque uma das circunferências com centro na origem e outra com centro no eixo das abcissas. A recta que passa pelos pontos de intersecção fica do tipo x=a (vertical). A intersecção com as circunferências fica fácil de determinar. No fim aplicam-se as transformações inversas.
Cumprimentos
:) E isso é (quase) a parte 3!
Enviar um comentário