Geometria analítica: rotações no espaço (1ª versão)

No espaço, as rotações são feitas em torno de uma recta orientada, a que vou chamar eixo de rotação.
A orientação da recta é importante para se poder ter também um sentido positivo para a rotação.

Comecemos com três rotações simples: as rotações em torno dos eixos coordenados:

Seja P um ponto do espaço, e R_Oz,θ a aplicação (ou função) que faz corresponder a P o ponto P′ do espaço correspondente a uma rotação em torno do eixo Oz, por um ângulo positivo de amplitude θ.

Exemplos:
R_Oz,(1, 0,-1) =
R_Oz, =
R_Oz, =
R_Oz, =
(z é um número real fixo);

Neste caso particular, consegue-se reaproveitar a fórmula do post anterior para rotações no plano, em torno da origem:

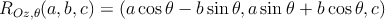
Ainda se consegue aproveitar esta fórmula para rotações em torno dos outros eixos. Uma rotação em torno do eixo Ox será R_Ox,θ e verificará a fórmula:

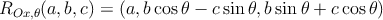
Da mesma forma uma rotação em torno do eixo Oy será R_Oy,θ

Passemos agora para o caso mais interessante, em que o eixo de rotação passa pela origem e tem a direcção de um vector arbitrário = (r_x,r_y,r_z).

Aqui o truque consiste em compor as aplicações anteriores.

Vou mostrar uma forma de efectuar a rotação(mas como poderão perceber, obviamente não é a única)

Seja α o ângulo que a projecção ortogonal de faz sobre o plano xOy, e φ o ângulo que faz com o semieixo positivo Oz

Então

(poderá querer fazer alguns esboços para se convencer disto)

E se o eixo de rotação for uma recta s, paralela a um eixo de rotação que não passa pela origem?

A essa rotação chamaremos R_s,θ. O problema resolve-se facilmente, de forma análoga ao caso das rotações no plano, fazendo uma translacção para um eixo que passe pela origem a que o eixo de rotação é paralelo, efectuando a rotação e desfazendo a translacção.

Observações:

• Nesta primeira versão, que pode-se considerar uma mera introdução evitei conscientemente alguns assuntos e alguns cálculos
• Um dia mais tarde penso que voltarei ao assunto ainda neste blog. Por isso deixei no título aquele "1ª versão"
• Nos próximos posts mostrarei algumas aplicações práticas destes dois últimos posts