Feliz 2015 a todos

2015 ... que seja um Novo ano, com novos projectos, novos sucessos, menos trapalhadas e certamente, melhor que 2014

http://www.portuguespt.com/

O Caderno...

Tenho, uma página no meu site pessoal, onde apresento alguns pdf's com minitextos meus...
Num desses pdf (Casio1999.pdf) tenho vários programas para calculadoras, (por exemplo os jogos Batalha Naval e CPmissil).
No entanto, nesse pdf está apenas o código não comentado dos programas (pois, as calculadoras têm um limite de memória que na altura me fazia tentar escrever o mínimo possível).
Transportei ambos os jogos para calculadoras recentes, (Nomeadamente, máquinas Casio fx-9860 e casio-Fx-CG20) E preparo-me para escrever versões mais recentes de ambos os programas no sdk oficial da Casio para a FX9860-G.
Ainda não está nos meus planos uma versão nova para CG-20, embora se justificasse (Nesta calculadora os jogos conseguem ser mais lentos do que para as calculadoras em que foram programados originalmente)

Na altura, quando escrevi os programas, tinha um caderno onde tomava registo de todos os raciocínios e variáveis , pois, naquelas máquinas todas as variáveis são globais, e portanto esse tipo de cuidado era necessário... Se o caderno ainda existir, um dia, deixo uma nova versão, dedicada ao pessoal que quiser aprender a programar coisas simples ou com uma complexidade limitada, na calculadora.
[Nessa altura, posso ainda transportar alguns dos programas para TI-83/84plus..]

Intersecção de Circunferências em coordenadas rectangulares Parte 2: A circunferência e a recta (I)

Sejam C(x₁,y₁) e M(x₂,y₂). Pretendo determinar os pontos de intersecção das circunferências de centro C e raio R₁ e de centro M e raio R₂, se existirem.
Portanto, pretendo obter uma expressão para as soluções do sistema

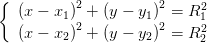
Desenvolvendo as equações temos:

E subtraindo a segunda equação da primeira temos:

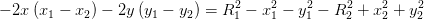
Esta última equação, é a equação de uma recta r que contem os pontos da intersecção das circunferencias. A equação mostra-nos que a recta r é perpendicular a CM, pois um vector ortogonal à   recta é Que é vector director de CM! Seguindo o exemplo que dei na primeira parte, para obter as coordenadas dos pontos de intersecção, se existirem, basta intersectar esta recta com uma das circunferências.

Resolver um sistema deste tipo é algo que até se faz bem... com números! Vamos lá espreitar o caso geral da intersecção de uma circunferência com uma recta:

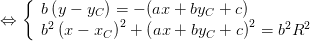
Não sei o leitor, mas a última equação já me dá alguma vontade de recorrer a um programa de computação algébrica, embora não sejam cálculos complicados.
No entanto como eu de vez em quando digo, quando se trata de implementação computacional, "por mais monstruosa que seja a fórmula...será o computador a tratar dela."
Note-se que no problema original da intersecção de circunferências o nosso a²+b² é o quadrado da distância entre os centros das circunferências.

Regressarei a este assunto, mas não para já...

Intersecção de Circunferências em coordenadas rectangulares Parte 1: um exemplo

Como foi visto na primeira parte do post sobre tangentes a uma circunferência que passam num ponto exterior, uma possível construção da solução passa pela intersecção de circunferências. Do ponto de vista da geometria analítica, estaremos perante uma tarefa fácil? Existirá uma forma geral "visualmente agradável" para a intersecção de circunferências?

Começarei com um exemplo simples: Quais as coordenadas dos pontos de intersecção das circunferências cujas equações são:

e

A minha sugestão, para resolver situações deste tipo é esta: desenvolvem-se os quadrados dos binómios de cada equação e subtraem-se as duas equações. A equação que resulta da subtracção, como veremos mais tarde, é a equação de uma recta perpendicular à recta que passa pelos centros das circunferências. Neste caso temos:

E subtraindo a segunda equação da primeira temos

Que é a tal recta, que contém os pontos de intersecção. Para determinar os pontos de intersecção, basta intersectar esta recta com uma das circunferências.

Ou seja:

Portanto

E esta é a técnica a seguir sempre. Infelizmente, seguir estes passos por forma a obter uma fórmula para o caso geral, tem o inconveniente de não nos dar uma fórmula muito amigável, como veremos na próxima parte.

---

PS: Não é propriamente necessário desenvolver os quadrados: se uma pessoa se lembrar que existe uma fórmula habitualmente designada por fórmula da diferença de quadrados, basta subtrair as equações iniciais...

Como foi visto no post do Sábado passado, a construção das rectas tangentes envolveu a intersecção de duas circunferencias.
Assim, neste fim de semana e na próxima semana, em vez de um post matemático serão postados dois (ou mesmo 3):
Um sobre intersecções de circunferências que será útil no futuro e depois então, o post com uma segunda parte sobre as rectas tangentes.

Estive a reescrever/recompilar/adaptar alguns dos meus programas (originalmente escritos no devc em windows) para Linux. Estão a funcionar bem, portanto a segunda parte do texto sobre as tangentes a circunferências que passam num ponto exterior deve ser postado em breve, dependendo da minha disponibilidade horária.

---

PS: Eu evito a tecnologia MathJax por exigir uma compilação em directo no servidor (...).
Primeiro escrevo um ficheiro LaTeX no computador, depois, converto para html recorrendo a um software livre que se encontra online, e finalmente, carrego as fórmulas pré-compiladas para um sítio na internet (tipicamente blogger ou picasa) e uso o programa linkreplacer que se vê a correr na animação ,(programa e animação da minha autoria, portanto, peço desculpa pelo erro de português na palavra construção) que analisa o ficheiro html e substitui os links para as imagens que tenho no computador por links para as imagens que estão online e depois de tudo isto copio o código html para o blog, ficando o post disponível online.

Dia cansativo... Acabei por adormecer no autocarro.
Vou ter de deixar o resto do problema para outro dia...

Rectas tangentes a uma circunferência que passam por um dado ponto exteriorParte I: régua e compasso

No post anterior deixei três desafios simples, e propus que após a resolução, se fizesse uma possível implementação em calculadora.
Vou resolver apenas um deles.
Dada uma circunferência de centro C e um ponto A exterior a ela, quais são as equações (completas ou, se possível, reduzidas) das rectas tangentes à circunferência que passam por A?

Vamos começar por esquecer a geometria analítica e resolver o problema geometricamente.
Deixo as justificações da construção que vou elaborar a cargo do leitor.
[Sugestão: basta a geometria que se aprende até ao fim do 9^oano de escolaridade]
Começamos por determinar o ponto M, ponto médio do segmento [AC].
Em seguida construímos a circunferência auxiliar de centro M e que tem como diâmetro o segmento [AC].
Esta circunferência intersecta a circunferência inicial em dois pontos, T₁ e T₂ que são os pontos de tangência das rectas que passam por A.
Note-se que esta construcção pode ser facilmente feita com uma régua e um compasso.

A geometria analítica fica para a próxima parte (Domingo ou Segunda, pois parece que tenho de rever o código de uma das aplicações que eu uso para postar Matemática aqui no blog..).
Segue-se uma animação da construção, feita com Geogebra...

Um exemplo de aplicação do que de vez em quando faço neste blog...

No dia 3 de Fevereiro deste ano, mostrei aqui no blog uma dedução de uma fórmula para a equação reduzida da mediatriz de um segmento.
Disse também que a fórmula poderia ser aplicada na elaboração de um programa para calculadoras... (ou mesmo para aqui para o blog).
No meu blog de explicações partilho algumas versões.
Podem ver na animação que se segue a versão para as CASIO CG10 e CG20

Deixo, como desafio deduzirem :

• a equação reduzida de uma recta tangente a uma circunferência num dado ponto da circunferência
• as equações das rectas tangentes à circunferência que passam por um dado ponto exterior
• uma equação cartesiana do plano mediador de um segmento no espaço.

E se houver tempo, escrevam código para uma calculadora (qualquer) e partilhem, pelo menos uma animação do programa a correr....

APM quer suspender Novos programas de Matemática do ensino secundário...

O Jornal Público noticiou na passada 4ª feira que a APM quer suspender o novo programa de Matemática do ensino secundário com base numa série de acusações.
Eu não sou lacaio do Ministro Nuno Crato (muito pelo contrário, critico muitas decisões dele), e muito menos da APM ou da SPM.
Não gosto desta "guerra"!
Eu tenho muitas reticencias  em ambos os programas.
Em primeiro lugar não me agrada ver uma coisa imposta "à acordo ortográfico", não gosto de várias coisas do actual. e quanto ao novo... ainda tem muitas arestas por limar. As acusações contra ou a favor dos novos programas são demasiado radicais para poderem ser levadas a sério, e quem vai nelas sem ter consultado a documentação de ambos os programas merece um bom e metafórico puxão de orelhas..

Quanto a essa história de "países de referência"... Para não ser mal educado, eu só vou dizer que Portugal está no estado em que está pelas muitas referências de outros..

Desde que uma petição com mais de 100 000 assinaturas  contra o AO não deu em nada que não me fio nelas...

Boa sorte à APM, com a sua petição.
Já agora eu recuso-me a assinar essa petição, apenas com base no texto com que é apresentada!

---

PS:Acabem com a palhaçada do radicalismo e dos "países de referência", porque estão é a mostrar ser da mesma classe que muitos políticos!
 Já me bastou o tal "limite universitário" do exame de 12º (1ª fase) do ano lectivo passado...
Ou a senhora Merkel a dizer que Portugal tem muito diplomado (!!!)

Calculadoras programáveis no ensino de Matemática...

Criei recentemente no meu blog de explicações uma página onde disponibilizarei programas para calculadoras.
Mas o grande problema é: o que é que se pode/deve deixar a um aluno do ensino secundário que pode levar uma calculadora para os testes ou mesmo para o exame?
Eu não gosto que as CASIO fx-9860GII, fx-CG10, CG 20 apresentem os valores exactos das razões trigonométricas de 30º, 45º e 60º pois é suposto um aluno de Matemática A de 11º sabê-las (e já agora explicar o porquê daqueles valores...).
Mas, com um mínimo de inteligência, qualquer aluno com uma calculadora científica consegue saber os valores exactos sem recorrer a cábulas.

Portanto, não gosto, mas consigo aceitar.
Já agora, continuando no 11º ano, eu escrevi um programa para calculadoras Texas e Casio que faz as reduções ao 1º quadrante, até desenhando os círculos...
Não passo o programa para os alunos (nem devem encontrá-lo no meu blog), mas não tenho problemas em escrever uma aplicação que corra no blog que faça o mesmo. Isto porque é suposto os alunos saberem fazer, e durante um teste, a menos que algo muito anormal se passe, não têm acesso ao blog....
Tendo um software que faça as reduções, o software serve de apoio ao estudo..
Tendo o software na calculadora num teste, o software substitui a capacidade de raciocínio do aluno.
Estando nós na época da Internet.. nada me garante que outros não o façam e coloquem online para depois os alunos instalarem nas suas calculadoras e terem o exercício resolvido pela calculadora.
Está bem, é algo simples... e a maioria dos alunos sabe fazê-lo.
Será? Muitos dos alunos de 11º que me pedem explicações têm inicialmente sérias dificuldades em ir ao círculo trigonométrico... e mesmo alguns de 12º não sabem!

Um terceiro exemplo, é a fórmula resolvente das equações de 2º grau. Hoje em dia muitas calculadoras já vêm com a fórmula pré-programada, e por uma questão de justiça, acabo por partilhar um programa para isso para que todos  fiquem em pé de igualdade, mas... vamos lá pensar um pouco.
A fórmula resolvente é dada no 9º ano.
E por algum motivo que nunca percebi, a fórmula também aparece nos formulários dos exames desse mesmo 9º ano. Não é suposto os alunos saberem a fórmula?

Parece que não... basta saber utilizar!?
E no ano seguinte 10º passam a ter uma calculadora que faz sozinha, fazendo com que um aluno consiga chegar ao 12º sem saber a fórmula resolvente (e atenção que eu já vi isso acontecer...)!
[Então e o estudo da função quadrática?].

Há muitos mais exemplos...
Não vejo com bons olhos a obrigatoriedade do uso de calculadora gráfica (programável) no ensino secundário. Uma calculadora que para a maioria das famílias está bem longe de ser barata!
(Note-.se que nem todos os alunos andam com telemóveis de 300-500€...)

Certos conhecimentos simples devem ser adquiridos e não ficar dependentes de tecnologia. A excessiva dependência de tecnologia em Matemática no ensino secundário não é necessária!

Eu gostava mais do skype antes de ser microsoft...

A piada é os meus contactos verem-me online sem eu ter sequer telemóvel, tablet ou computador ligado.

---

Enfim... Ao fim de várias tentativas lá consegui recuperar a minha conta.

Ando a desperdiçar recursos....

Esta imagem faz-me pensar na quantidade de urina que ando a desperdiçar há anos quando podia vendê-la como matéria prima para a produção de uísque (Será que em português correcto se aceita que eu diga whisky?...)

---

PS: Não pesquisei a veracidade desta informação, mas pode servir para fazer algumas pessoas pensar duas vezes antes de beber...

A nova versão...

(Gabinete do professor Xabe Bué Bué)
-Bom dia professor ! É o professor que vai leccionar a cadeira 4anosParaPassarUm?
-Olá! Sim vou substituir o professor Xabia Mais Do Que Eu. A cadeira vai mudar de nome, vai passar a chamar-se 5AnosParaPassarUm. Eu fiz umas alterações no programa que justificam a mudança de nome.
-Ah... é que eu vou inscrever-me em época especial de finalista.
-Sim, também sou eu a fazer o exame dessa cadeira, já que infelizmente o professor faleceu..
-E o programa para o exame, ainda é o da versão anterior da cadeira não é?
-Sim, como dizem os regulamentos, é.
-Se eu chumbar vou ter de fazer a versão nova da cadeira?
-Oh menino! Vai por-me a fazer um exame para chumbar?
-Nãão..É mesmo só para o caso...
-Nem ponha essa hipótese. Até vou dar-lhe uma dica, estude o capítulo 2 do meu livro: ComIstoNãoChegaLá.
-Posso passar os olhos?
-Sim passe... (o aluno passa os olhos pelo livro)
-Eh...Isto estava no programa antigo?
-Sim, sim, estava subentendido no capítulo 299, secção 120 parágrafo 149 do programa anterior..
-Ah bom...! Vou para casa estudar. Obrigado pela dica!
 ( e sai a correr como se tivesse tido uma revelação)
-Estes miúdos...deixam tudo para a última hora...
Por falar nisso.. só me falta a bibliografia da minha versão da cadeira.
As vendas do meu livro ComIstoNãoChegaLá estão em baixo... este tem mesmo de ir para a bibliografia.
O volume 2, ComIstoTambémNão, serve de complemento.
Para reduzir as dúvidas de NãoPerceboIsto vou por o livro do DontRead MyBooks. Espero que não tenham medo de ler bibliografia estrangeira, afinal são estudantes de ensino SubSuperior.
Deixa cá ver a bibliografia do meu antecessor...
Pá! Isto ninguém lê! O livro do PassaTodos tem erros científicos e está ultrapassado!
Estes são bons, vou copiar.
Como é uma cadeira de Matemática, vou por ainda o livro do Campos Ferreira, o Apostol, o Piskunov, e o se calhar o Lang, e o Brézis  ...
(knock knock)
-Entre!
-Oh! Zé Ninguém! Estou aqui a acabar o programa de 5AnosParaPassarUm... diz-me o que achas!
(olhando para o programa e para a bibliografia...)
-Pá, os últimos livros acho que podiam ser substituidos por livros "clássicos" mais recentes!
-Por exemplo, o Mecânica Analítica de Lagrange, o Princípia Mathematica de Newton, o Elementos de Euclides, a última edição do Spiderman,  já agora também a última da Supergirl e não ficava nada mal uma edição qualquer do Rato Mickey ou do Tio Patinhas. E ali, na secção que ninguém lê, o livro ExcelenteParaPassarEstaTrampa do CadeiraEmSaldos.
-Excelentes sugestões! Vou juntá-las já! Já agora, o que é que achas da cadeira?
-Pá...sendo uma cadeira de 1º ano, penso que os de 5º ano vão conseguir fazê-la..
-Pois.. eu já disse várias vezes que esta cadeira devia estar no 5º ano, mas aqui ninguém me ouve... Já agora,  a que devo o prazer da visita?
-Vinha convidar-te para irmos à feira do livro...
-Ah... boa ideia!
Ao sair...
-Olha... Achas mesmo que o livro do CadeiraEmSaldos é boa ideia?

Haja paciência...

Tenho uns familiares engraçados... daqueles que gostam de se intrometer na vida dos outros, dar "opiniões" que mais parecem ordens.
Eu passei a evitá-los há anos, mas às vezes vejo-os a fazer das suas com outros familiares meus!
Irónico foi ver descrições completamente distorcidas de coisas a que eu testemunhei e eles não, a sair daquelas bocas!
Andam a criar confusões e mal estar à minha volta! Esta gente não tem vida ou o quê?
Eu não suporto intriguistas!

No futuro, uma das vezes que este blog ficar parado será por eu porque eu ter ficado mesmo aborrecido, ter dado uns tabefes em alguém e ido parar umas noites a uma esquadra ou qualquer coisa do género.

Enfim...

Falar do 5 de Outubro e da implantação da República?
Tenham juízo! Não sou monárquico, mas tenho de reconhecer que a república que temos em Portugal é uma vergonha! Já devia ter caído há anos, e dado lugar ou a uma 4ª república ou a outra coisa qualquer... de preferência, melhor!

A flexibilidade dos malu...isto é, matemáticos

Para além de explicações ando a trabalhar noutras coisas.
São os meus planos B.
A verdade, é que o meu conhecimento de Matemática e de outras áreas... um pouco mais vasto do que o que de facto aprendi em qualquer instituição de ensino superior permite-me "esticar-me" para vários lados...
Nos tempos que correm, a criatividade e a capacidade de sobrevivência são virtudes.
Mas não posso esquecer que a minha saúde é uma bomba-relógio marcada aleatoriamente... assim como a vida de todo o cidadão vivo à face da Terra.

Como qualquer português, o meu maior desafio, que consegue ser maior que o desafio da sobrevivência é conseguir ganhar dinheiro sem ser roubado pelo Estado.

A minha flexibilidade permite-me fazer muita coisa, que, estupidamente, pouca gente tem noção... Portanto, tenho de ser eu a "lançar-me" de cabeça em qualquer projecto, tendo o cuidado de ter sempre um ou dois para-quedas à mão...O problema é que estes para-quedas começam a ser difíceis de encontrar.

É Sábado... é noite... e eu estou sentado à frente do computador a escrever num blog...

Pois... deve ser o preço dessa tal flexibilidade.

Novo filme da PIXAR

Inside Out US Teaser Trailer:


(É assim que se arranja coragem para acordar cedo ao Sábado e ir trabalhar)

Stop

Ontem notei que há dois anos que não dou explicações a grupos de alunos de estabelecimentos de ensino superior daqui, mas tenho tido procura e sucesso com alunos de fora. Tanto que nunca me preocupei em tabelar valores, e inadvertidamente, ontem apresentei os preços cobrados a pessoal de fora a alunos daqui, e obviamente "mandaram-me passear".

Mas de facto... os meus preços são caros para alunos que não trabalham, que provavelmente estão a ser os pais a pagar estudos.
(E, por outro lado, tirando situações pontuais, não estou a ver muitos bons motivos para um aluno de superior recorrer a explicações, mas já conheço alguns bons e válidos )
Por outro lado algumas pessoas, que até pagaram, consideraram barato... para o tipo de serviço que eu presto.
Portanto, estou seriamente a considerar a hipótese de  recusar pessoal de superior daqui e abandonar aquilo que até hoje tem sido a minha política (principalmente para alunos da UMa): negociar com grupos.

Alguém interessado?

Uma vez que no presente ano lectivo fui forçado a reduzir drasticamente o meu horário na Casa do Povo da Camacha e também há necessidade de alguém para explicações de Física e Química...
Há alguém interessado em ser meu colega por lá?

Knock Knock

Este é certamente um dos vídeoclips mais bem feitos que já vi 

Brunettes Shoot Blondes - Knock Knock (Official Video) from Brunettes Shoot Blondes on Vimeo.

Um esquema de Hiparco

No blog que serve de apoio a algumas das minhas explicações deixei um problema inspirado numas notas que escrevi pouco depois de terminar o 9º ano (Não conheço muita gente como eu... portanto devo ser anormal...)

http://cpexplicamatematica.blogspot.pt/2014/09/do-esquema-de-hiparco-ao-cosseno-do.html

Sugiro o problema aos bons alunos que terminaram o 9º ano e aos alunos de 11º ainda antes de serem apresentados ao círculo trigonométrico.

---

PS: Note-se que aquele mesmo esquema pode ser usado para deduzir o valor de sin (2α)

Bash

Tenho imensos shell-scripts escritos para me facilitar a vida... muitos deles em bash!
Portanto, notícias destas :http://exameinformatica.sapo.pt/noticias/internet/2014-09-25-Bash-o-bug-que-pode-gerar-mais-problemas-do-que-o-Heartbleed deviam preocupar-me.
Só que... já estou habituado ao jornalismo sensacionalista (que confesso ser algo que eu ainda detesto mais do que o Acordo Ortográfico). E depois... bem, Linux, ou mesmo MacOS não são Windows!

Atenção: segundo consta, esta actualização ao bash não resolve todos os problemas mas já dá uma maior segurança. Se está ligado à Internet mantenha o seu sistema actualizado, seja ele qual for, pelo menos em assuntos de segurança!

Ofertas perigosas

De acordo com a exame informática a Microsoft oferece mais 15 GB aos utilizadores móveis que activarem o backup automático das fotografias para a nuvem.
Hum... "backup automático de fotos", por favor corrijam-me nos comentários se eu estiver enganado...
mas não foi uma funcionalidade deste tipo que acabou por estar na origem do escândalo das fotos de celebridades? Um hacker( ou um grupo de hackers...) que entrou nos backups automáticos feitos para a iCloud?
Eu até agradeço os 15 Gb extra, espaço extra dá sempre jeito, mas "backup automático de fotos para a nuvem" não me convence.
Eu não tenho fotos privadas escandalosas, mas são privadas, e pergunto-me se o risco de se tornarem públicas compensa...
Por exemplo, toda a gente tem fotos de filhos, netos, enfim, crianças, que certamente não gostaria de ver públicas na Internet, nos olhos de completos desconhecidos (sim, concordo que é discutível, mas penso que os encarregados de educação deviam ao menos poder escolher os desconhecidos...)

Preços de Explicações:Comparar o que é incomparável

Ao estabelecer preços de explicações, os números de horas, e os números mínimos e máximos de alunos numa sala tenho sempre várias coisas em conta:

• O rendimento escolar dos alunos
• A necessidade de os alunos saírem capazes de abordar o máximos de situações
• As despesas com os locais/intermediários
• O tempo gasto na preparação do Material
• Os tempos que se perdem com eventuais distracções
• O lucro mínimo aceitável ( explicador também paga impostos e segurança social... ou foge e está ilegal até ao dia em que a fiscalização lhe cai em cima com multas na ordem dos milhares de euros)

Para os ensinos secundário e superior, em vez dos tempos de hora e meia que são típicos, sempre preferi os tempos de duas horas, por motivos que não vou especificar aqui...

Portanto, é absurdo comparar os preços de um explicador que leva no máximo 5 alunos numa sala, com os de um que leva 20 ou mais, tal como é absurdo comparar directamente preços de explicações com tempos de duas horas com preços de explicações de uma hora, ou uma hora e meia, ou mesmo explicações dadas no centro de Lisboa com explicações dadas no centro do Funchal.
Na verdade... podem-se estabelecer fórmulas ponderadas que permitem fazer comparações, mas isso nunca é feito por ninguém que compare preços!

Privacidade na internet...

O escândalo das fotos de celebridades obtidas por hackers, é algo que me faz na estupidez das pessoas.
O que foi feito é sem dúvida bastante indecente! Foi uma violação da vida privada dessas celebridades.

Mas serei eu o único a achar que se essas fotos não existissem isto provavelmente não teria acontecido?
Quero dizer... Se apenas existissem fotos banais, será que havia escândalo?

Claro que há que apontar o dedo não só ao hacker como também à apple e pedir esclarecimentos sobre como é que isto foi possível, mas...
Se apanharem o meu telemóvel garanto que não encontram nada de anormal.
Nem mesmo com qualquer software de recuperação! Portanto, a ideia de haver uma sincronização entre qualquer dispositivo meu eu e a Internet não me preocupa assim tanto (mas preocupa, bolas, tenho direito à minha privacidade)!

Felizmente não sou uma celebridade, e penso que estou bem longe disso...

Chamadas não atendidas...

Não há mesmo melhor solução.
Sempre que quero trabalhar e tenho trabalho atrasado, a melhor solução é mesmo tirar o som ao telemóvel/desligar.
Só ontem, eu tinha uma dezena de sms's no telemóvel, e nem digo quantas chamadas não atendidas...
E nenhuma era a pedir explicações!
Eu tenho vários projectos meus em mãos, e se não me aparece nenhuma proposta melhor a nível profissional, vou avançar com eles.
Quais são?
Peço desculpa. O segredo é a alma do negócio...
Não se preocupem se eu não der notícias! Passem por um dos meus blog, vejam se deixei alguma coisa interessante escrita!
Cliquem ali no visitei recentemente, vejam se há coisas novas, ou então vejam só se deixei alguma coisa partilhada no facebook.

Não se preocupem! Não tenciono desaparecer como o meu amigo! Mas deixem-me trabalhar!
[Bolas... agora eu parecia o Cavaco Silva...]


PS: Ver se há posts novos realmente é capaz de falhar... Posts, como por exemplo este de hoje, foram agendados dias antes.

Os "gosto" do facebook

Ontem ao visitar este post do meu blog dedicado às explicações notei uma coisa fantástica: O número de gostos tinha sido reduzido a zero!
Ora.. no dia antes o número rondava os 24. Espero que ninguém tente convencer-me que de repente todas as pessoas que clicaram gosto foram lá eliminar o seu "gosto"!
O texto não sofreu alterações muito significativas desde que foi postado, nem estou a ver uma razão suficientemente forte para acontecer uma coisa destas (por outro lado, até na coluna do lado direito deste blog tenho um link directo para esse post, portanto, é normal o número de "gosto" ir aumentando.
O que se passa, é que estas contagens são feitas por um algoritmo que as guarda em bases de dados...
Basta um erro informático qualquer ou uma alteração no código do facebook que as contagens vão todas ao ar.
Na verdade, o número "gosto" não dá grande informação. O número de visitas à página por clique directo ronda neste momento as 90, e as visitas ao blog que não identificam o texto que o leitor tem à sua frente apresentam (naturalmente) um número muito maior.

Note-se que este é o único dos posts desse blog que sofreu uma redução brutal.

Mesmo aqui, no CarlosPaulices no século XXI, os gostos continuam intactos...

Que se lixe.. ao menos posso criar uns exercícios engraçados de probabilidade condicionada com isto!

Procura-se

Ao que parece, o meu amigo, colega professor e explicador de Matemática Ricardo Alho está desaparecido há alguns dias.
 Várias pessoas no facebook partilharam uma mensagem a pedir a quem souber do seu paradeiro que informe a família ou a PSP.

(A foto tem um link para uma dessas mensagens...)

Olá Setembro

Para ser 100% honesto, a imagem eu encontrei no facebook! O verdadeiro desabafo é este: A cada arraial que passa eu odeio cada vez mais os arraiais...

Adeus senhor Williams

             Era suposto o blog estar de férias, mas a morte de Robin Williams, é demasiado chocante para deixar em branco. Tentei não comentar as mortes de Steve Jobs, ou de Nelson Mandela, mas o caso do Senhor Williams, e senhor com um S grande, não dá...
            Estamos a falar de um artista que se destacou em vários tipos de papeis, mas que me fez dar valentes gargalhadas.
De todos os excelentes filmes em que entrou vou destacar apenas um: o homem bicentenário, baseado na obra de Isaac Asimov.
           A nível de crítica,.. bem estamos na era da internet! Chego, por exemplo ao IMDB e leio muita m****, de críticos improvisados, "comentadores de bancada".
Que se lixem as opiniões dos outros. Eu adoro o filme! Tenho-o em DVD, e é daqueles que não me canso de ver.
          Também gosto do "Bom rebelde", mas... sinceramente, prefiro este.

As histórias de depressão e suicídio, chocam-me. Um homem que fez tanta gente rir passou anos a lutar com uma depressão.
Acho que a melhor forma de combate à depressão é evitar idiotas* , e distraindo-se.

Há por aí muita gente que se mete em assuntos que não são seus e estragam a vida dos outros, causando depressões, suicídios e outras desgraças.

Senhor Williams, onde quer que esteja, espero que esteja feliz, e continue a fazer rir/animar os outros, porque sem isso a vida é um pesadelo!
Até um dia!

---

* Eu posso chamar um conjunto de coisas piores, mas não quero ter de marcar este blog para maiores de 18 anos por linguagem imprópria.

Blog de férias até Setembro

Quem vai entrar de férias é este blog e não eu.
Estou neste momento a tratar de alguns projectos e ideias, e vou aproveitar o mês de Agosto para isso.
Em princípio só volto cá em Setembro, mas nunca se sabe.

Caso algum leitor pretenda contactar-me, pode sempre mandar-me um email, e terá uma resposta logo que for possível.


Bom mês de Agosto para todos.

(censurado)

      Uma das atitudes mais arrogantes de muita gente de várias religiões e crenças é acreditar que a de impor as suas crenças a quem não as pediu. No caso de religiões onde existe um livro central, ainda é mais arrogante por-se a citar passagens do livro e impor a sua interpretação a outros que não estão interessados.
     Este tipo de pessoas são o que há de mais podre à face da Terra...
A ciência não é bem uma religião, mas também há cientistas com estas características.